无人机编程：奥数和编程教育相辅相成！~济南无人机编程~山东无人机编程

    奥数这门学科，仿佛是学霸的代名词，因为只有学霸才开始学习奥数。但是我们今天说的是编程和奥数相辅相成，如果学了编程，奥数几乎没有难度！

    奥数本质是什么？1.模式化的解题；2.强化练习的记忆。奥数题都是有模式的，就是把具体问题抽象化后总结的解题方式，加上强化解题训练，只要是正常智商的儿童都能够学会。

    先总结一下模式

    一、归一问题

    基本特点：问题中有一个不变的量，一般是那个“单一量”，题目一般用“照这样的速度”……等词语来表示。

    关键问题：根据题目中的条件确定并求出单一量。

    二、鸡兔同笼问题

    又称置换问题、假设问题，就是把假设错的那部分置换出来。

    基本思路：

    ①假设某现象存在（甲和乙或乙和甲一样）

    ②假设后，发生了和题目条件不同的差，找出这个差是多少

    ③每个事物造成的差是固定的，从而找出出现这个差的原因

    ④再根据两个差作适当调整，消去出现的差。

    基本公式：

    ①把所有鸡假设成兔子：鸡数＝（兔脚数×总头数－总脚数）÷（兔脚数－鸡脚数）

    ②把所有兔子假设成鸡：兔数＝（总脚数一鸡脚数×总头数）÷（兔脚数一鸡脚数）

    关键问题：找出总量的差与单位量的差。

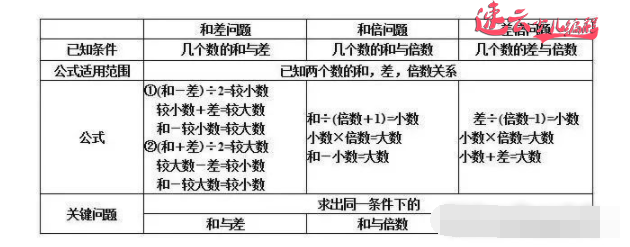
    三、和差倍问题

    四、盈亏问题

    基本思路：先将两种分配方案进行比较，分析由于标准的差异造成结果的变化，根据这个关系求出参加分配的总份数，然后根据题意求出对象的总量．

    基本题型：

    ①一次有余数，另一次不足的基本公式：总份数＝（余数＋不足数）÷两次每份数的差

    ②当两次都有余数的基本公式：总份数＝（较大余数一较小余数）÷两次每份数的差

    ③当两次都不足的 基本公式：总份数＝（较大不足数一较小不足数）÷两次每份数的差基本特点：对象总量和总的组数是不变的。

    关键问题：确定对象总量和总的组数。

    五、植树问题

    六、经济问题

    利润的百分数=（卖价-成本）÷成本×100%

    卖价=成本×（1+利润的百分数）

    成本=卖价÷（1+利润的百分数）

    商品的定价按照期望的利润来确定

    定价=成本×（1+期望利润的百分数）   

    本金：储蓄的金额 利率：利息和本金的比 利息=本金×利率×期数

    含税价格=不含税价格×（1+增值税税率）

    七、 工程问题

    基本公式：

    ①工作总量=工作效率×工作时间

    ②工作效率=工作总量÷工作时间

    ③工作时间=工作总量÷工作效率

    基本思路：

    ①假设工作总量为“1”（和总工作量无关）

    ②假设一个方便的数为工作总量（即完成工作总量所用时间的最小公倍数），利用三个基本关系，表示出工作效率及工作时间。

    关键问题：确定工作量、工作时间、工作效率间的两两对应关系。

    八、数列求和等差数列

    首项：等差数列的第一个数，一般用a1表示

    项数：等差数列的所有数的个数，用n表示

    公差：数列中任意相邻两个数的差，用d表示

    通项：表示数列中每一个数的公式，用an表示数列的和：这一数列全部数字的和，用Sn表示基本公式：

    通项公式：an = a1+（n－1）d

    通项＝首项＋（项数一1) ×公差

    数列和公式：sn,= (a1+ an)×n÷2

    数列和＝（首项＋末项）×项数÷2

    项数公式：n= (an+ a1)÷d＋1

    项数=（末项-首项）÷公差＋1

    公差公式：d =（an－a1））÷（n－1）

    公差=（末项－首项）÷（项数－1）

    九、综合行程问题

    基本公式：路程=速度×时间

    路程÷时间=速度

    路程÷速度=时间

    相遇问题：速度和×相遇时间=相遇路程

    追及时间＝路程差÷速度差

    流水问题：

    顺水行程=（船速+水速）×顺水时间

    逆水行程=（船速-水速）×逆水时间

    顺水速度=船速+水速

    逆水速度=船速-水速

    静水速度=（顺水速度+逆水速度）÷2

    水 速=（顺水速度-逆水速度）÷2

    流水问题：关键是确定物体所运动的速度，参照以上公式。

    过桥问题：关键是确定物体所运动的路程，参照以上公式。

    以上是一般模式总结，缺点显而易见——往往只加强了模式化训练，忽略了各个模式间的横向联系的思考。

    现实世界的问题没有单一模式，全部都是综合模式解决问题。举个例子——航空工程造飞机。

    飞机实际上就是多模式整合妥协优化的产物。

    思考几个问题，人类制造飞机要干什么？

    1. 缩短往返两地时间

    2. 载重运输

    那么缩短时间的方法有几个？

    1. 最直接的暴力的——增加发动机数量。

    2. 优化气动外观

    但是粗暴的直接增加发动机数量带来了更复杂的问题：1.破坏了气动外观，降低了速度或者增加了操纵难度，2.飞机承重结构承重能力有限，无法承载更多发动机

    怎么增加载重量？——最直接的方法增加体积。那么问题来了，材料承受自重的性能是有极限的，增加体积也意味着自重增加。增加体积也需要更大推力的发动机，但发动机性能有限，不能满足过大的体积（质量）的增加。

    所以从制造飞机来看，不能用单一模式思维去考虑问题，应该综合运用不同知识和模式去解决问题。

    少儿学编程就是为了弥补单一模式的不足。通过编程运用不同模式思维，把不同学科的知识横向关联起来解决问题，来拓展思维。从多角度抽象问题，最终得出优化结果，使知识更加贴合实际。

    例如足球机器人，他就涉及到了电子硬件知识（尤其是各种传感器）、机械知识、AI人工智能。而最终的编程就是要把前述的知识综合运用，充分发挥各部分的性能优势，最终取得胜利。

    速云少儿编程致力于 4 - 18 岁，山东少儿无人机编程教育机构，教给孩子们不光要学习编程，还要结合编程知识给我们无人机写程序，实现我们无人机的自动启飞、人脸识别、智能跟随，包括更加高级的编程玩法，就是无人机编舞。可能家长想了！四岁孩子能学习无人机编程吗？那我们看个四岁的小同学吧，你自己看看能不能学习吧！

我们来看一看四岁小朋友的学习视频吧！

    家长担心孩子们真的能听懂课程吗？在每节课即将结束的时候我们都会进行课程汇报展示，来看一下小童鞋的汇报成果吧！

    这个时候家长可能说了，我们四岁的孩子，年龄辣么小，又不认字，那该如何学习呢？

    其实四岁、五岁的孩子不认字怎么学习？只要孩子识别颜色就可以学习。通过颜色识别具体编程积木，比如：蓝色是运动、紫色是外观、黄色是事件等等，通过颜色识别文字，根据颜色先实现出程序做出卡通的效果，以激发孩子兴趣，使孩子产生兴趣后开始具体学习每个积木的作用，再学习积木上面的文字。如下图：

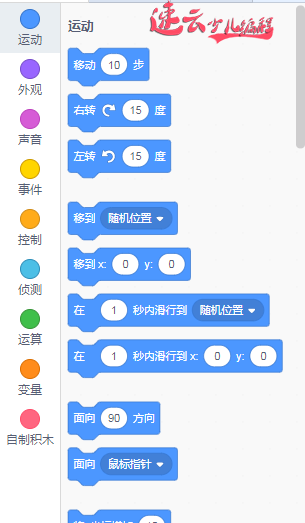
    这个时候你还认为编程难吗？其实针对4岁起，就已经可以学习编程了。通过搭积木的方式让孩子学习编程。

    当然，比如我们下面的无人机编程视频吧！

    无人机能六架一起起飞？没错！那他又和数学有什么关系呢？

    小云说啦！这是根据我们数学中的坐标轴的 x轴 y轴 初始化无人机位置，无人机与无人机之间的距离、架数的多少，全部需要通过精密的计算，否则无法编排出理想的造型。

    现在作为家长的你！还在纠结无人机编程是否对孩子有帮助吗？

无人机编程能做什么？人脸识别？智能跟随？自动飞行？还有吗？

答案：有！那就是"无人机编舞"！不知道无人机如何编舞？快看下面我们速云小童鞋的无人机编舞吧！！

    无人机编程都学习哪些内容呢？

       让无人机与编程结合？

没错！就是要让孩子“动手”+“编程”实现无人机起飞。

重点培养孩子逻辑思维能力与动手操作能力，让孩子在编写无人机程序的时，无形的锻炼孩子的逻辑思维能力和前沿科技的运用能力，在飞行学习中，孩子们需了解飞机的机械结构，练习手眼协同能力，甚至自己组装飞行器；在编程中，无人机可以在三维空间中，用摄像头完成巡线、人脸识别等人工智能任务。

例如：人脸识别，智能跟随，红外线定稿，光流定位、无人机编舞等。

看我们小童鞋们上课视频吧

    坦克编程都学习哪些内容呢？

    动手组装”+“编写程序”

    通过编程将抽象理论与实践操作合二为一，让孩子重新理解知识，体验人工智能，培养独立思考的习惯和动手解决问题的能力。

    课程涉及机器人拼装、力学等数理知识，运用六类人工智能模块，编写专属的自动驾驶算法程序，让孩子更加深入理解人工智能技术。

    例如：人脸识别、智能跟随等前沿技术。